概要
教師なし学習を使った異常検知をやってみたいと思い 、Pythonではじめる教師なし学習を読んでいたらちょうど いいお題があったのでやってみることにした
ここではサンプルデータを対象にPCAを使った異常検知を行う
なぜ検出できるのかという理論的な内容についてはここでは触れない。(というかわかっ てない)
アプローチ
PCAについて はこのPDFが 詳しく書いてあった
前提として、なんらかの理由で訓練データに異常標本が混ざっており、教示データを用意 できないこととする。
(専門家の方には怒られてしまう表現なのは重々承知で、)
上記の資料ではPCAは以下のように説明されている
多次元データのもつ情報をできるだけ損わずに低次元空間に情報を縮約する方法
この性質を使って、
- 異常標本が混ざっている多次元データ
- 1のデータをPCAで次元圧縮し、固有値ベクトルを取得
- 1と2のデータを使って一度次元圧縮し、復元した逆変換データを作る
- 元データと逆変換データの差分が大きい値を異常標本として検出する
上記のような処理をすることで、一度PCAをした際に正常なデータの方が多いことが想定されるため、Fitされるベクトルが正常標本に偏りと思われる
その性質を利用して、逆変換をした際に異常標本は正常データに偏って変換されるため元データとの差分が正常標本よりも大きくなると考えられる
PCA を使った異常検知の実装
2値分類のサンプルデータを生成
from pyod.utils.data import generate_data
X_train, _, y_train, _ = generate_data(
n_train=2000,
n_test=0,
contamination=0.1, # percentage of outliers
random_state=42,
)X_trainとy_trainの中身
X_train:
(2000, 2)
[[6.43365854 5.5091683 ]
[5.04469788 7.70806466]
[5.92453568 5.25921966]
[5.29399075 5.67126197]
[5.61509076 6.1309285 ]]
y_train:
(2000,)
[0. 0. 0. 0. 0.]以下は入力データの分布の画像だが、特徴量を見ても別のデータとして視認できそう
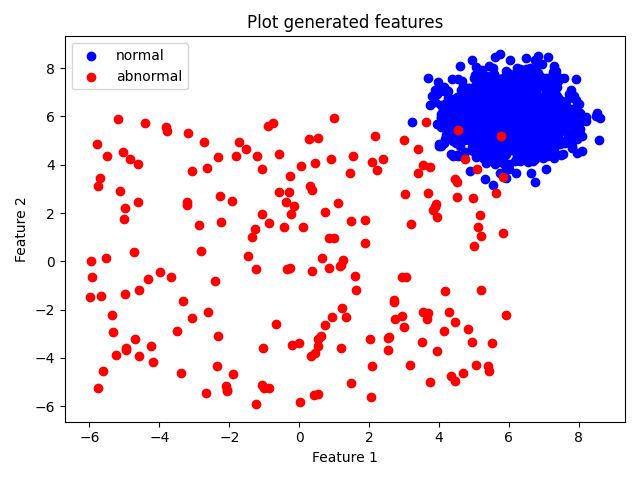
PCA を使ってデータを逆変換
import numpy as np
from sklearn.decomposition import PCA
def fit_and_inverse(data: np.ndarray, n_components: int = 2):
pca = PCA(n_components=n_components)
reduced = pca.fit_transform(data)
inverse = pca.inverse_transform(reduced)
return inverse
raw = X_train.copy()
inv = fit_and_inverse(raw)元データと逆変換データの差分から閾値を決定
mse = ((raw - inv) ** 2).mean(axis=1)
# NOTE:
# 今回は10%が異常データとして生成してるので90percentileで閾値を設ける
# 実際には想定される異常値の割合や期待する再現率などから設定すると考えられる
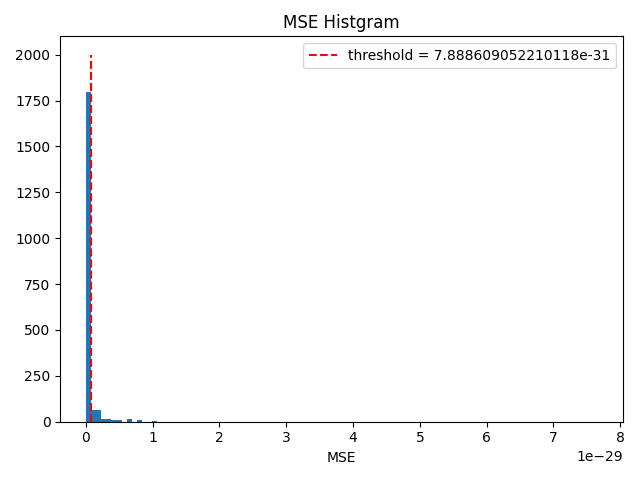
threshold = np.percentile(mse, 90)以下の画像が標本ごとのMSEの分布と閾値になる
分布からはこれが良い閾値なのかはわかりにくいと思った
分類結果
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| 1.0 | 0.91 | 0.70 | 0.79 | 200 |
| 0.0 | 0.97 | 0.99 | 0.98 | 1800 |
まとめ
PCAを使った異常検知の手法ということで、ラベルデータがない環境下でも取れる手段としていい知見になった。
使っている手法がPCAになるのでカテゴリカルデータや元データの次元数が多い時などさまざまな場面では制約になることがあるのかなあとか思った。
See Also
Support
もしこの記事が役に立ったなら、 こちらから ☕ を一杯支援いただけると喜びます